Разрезание на две равные части, часть первая
Задачи на разрезание — это та область математики, где, как говорится, мамонт не валялся. Множество отдельных проблем, но по сути нет общей теории. Помимо всем известной теоремы Бойяи-Гервина, других фундаментальных результатов в этой области практически нет. Неопределённость — вечный спутник задач на разрезание. Мы можем, например, разрезать правильный пятиугольник на шесть частей, из которых можно сложить квадрат; однако мы не можем доказать, что пяти частей для этого было бы недостаточно.
С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.
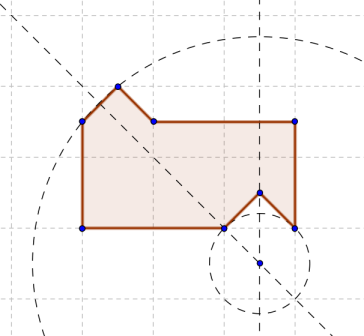
Введение
Для начала освежим школьный курс геометрии и вспомним, что такое равные фигуры. Яндекс услужливо подсказывает:
Две фигуры на плоскости называются равными, если существует движение, взаимно однозначно переводящее одну фигуру в другую.
Теперь расспросим Википедию про движения. Она расскажет нам, во-первых, что движение — это преобразование плоскости, которое сохраняет расстояния между точками. Во-вторых, там даже приведена классификация движений на плоскости. Все они относятся к одному из следующих трёх типов:
- Параллельный перенос
- Поворот
- Скользящая симметрия (сюда я удобства ради и пользы для включаю зеркальная симметрию, как вырожденный случай, где параллельный перенос производится на нулевой вектор)
Введём некоторые обозначения. Разрезаемую фигуру мы будем называть фигурой A, а две гипотетеческих равных фигуры, на которые мы будто бы можем её разрезать, обзовём B и C соответственно. Часть плоскости, не занятую фигурой A, мы назовём областью D. В тех случаях, когда в качестве разрезаемой фигуры рассматривается конкретный многоугольник с картинки, мы будем называть его A0.
Так вот, если фигуру A можно разрезать на две равных части B и C, то существует движение, переводящее B в C. Это движение может быть либо параллельным переносом, либо поворотом, либо скользящей симметрией (начиная с этого момента, я больше не оговариваю, что зеркальная симметрия также считается скользящей). На этом нехитром и, я бы даже сказал, очевидном, базисе и будет строиться наше решение. В этой части мы рассмотрим самый простой случай — параллельный перенос. Поворот и скользящая симметрия попадут во вторую и третью часть соответственно.
Случай 1: параллельный перенос
Параллельный перенос задаётся единственным параметром — вектором, на который происходит сдвиг. Введём ещё несколько терминов. Прямую, параллельную вектору сдвига и содержащую хотя бы одну точку фигуры A, будем называть секущей. Пересечение секущей прямой и фигуры A будем называть сечением. Секущую, относительно которой фигура A (за вычетом сечения) целиком лежит в одной полуплоскости, будем называть границей.
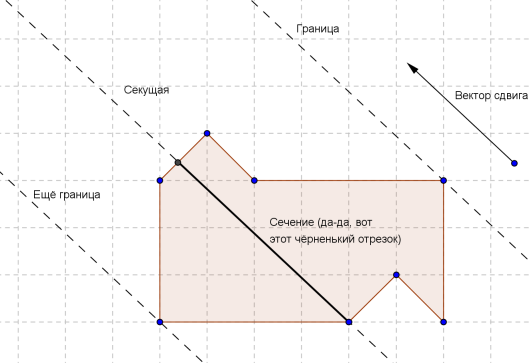
Лемма 1. Сечение границей должно содержать более одной точки.
Доказательство: очевидно. Ну или более развёрнуто: докажем от противного. Если эта точка принадлежит фигуре B, то её образ (т.е. точка, в которую она перейдёт при параллельном переносе) принадлежит фигуре C => образ принадлежит фигуре A => образ принадлежит сечению. Противоречие. Если эта точка принадлежит фигуре C, то её прообраз (точка, которая при параллельном переносе перейдёт в неё) принадлежит фигуре B, и далее аналогично. Получается, в сечении должно быть хотя бы две точки.
Руководствуясь этой нехитрой леммой, нетрудно понять, что искомый параллельный перенос может происходить лишь вдоль вертикальной оси (в текущей ориентации картинки) Если бы он был в любом другом направлении, хотя бы одно из граничных сечений состояло бы из единственной точки. Это можно понять, мысленно повращав вектор сдвига и посмотрев, что при этом происходит с границами. Чтобы исключить случай вертикального параллельного переноса, нам понадобится более хитрый инструмент.
Лемма 2. Прообраз точки, находящейся на границе фигуры C, находится либо на границе фигур B и C, либо на границе фигуры B и области D.
Доказательство: неочевидно, но сейчас мы это исправим. Напомню, граничной точкой фигуры называется такая точка, что сколь угодно близко от неё найдутся как точки, принадлежащие фигуре, так и точки, не принадлежащие ей. Соответственно, вблизи граничной точки (назовём её O’) фигуры C найдутся как точки фигуры C, так и другие точки, принадлежащие либо фигуре B, либо области D. Прообразами точек фигуры C могут быть только точки фигуры B. Следовательно, сколь угодно близко к прообразу точки O’ (будет логично назвать его точкой O) найдутся точки фигуры B. Прообразами точек фигуры B могут быть любые точки, не принадлежащие B (то есть либо точки фигуры С, либо точки области D). Аналогично для точек области D. Следовательно, сколь угодно близко к точке O найдутся либо точки фигуры C (и тогда точка O будет на границе B и C), либо точки области D (и тогда прообраз на границе B и D). Если вы сумеете продраться через все эти буквы, то согласитесь, что лемма доказана.
Теорема 1. Если сечение фигуры A представляет собой отрезок, то его длина кратна длине вектора сдвига.
Доказательство: рассмотрим «дальний» конец этого отрезка (т.е. тот конец, прообраз которого также принадлежит отрезку). Этот конец, очевидно, принадлежит фигуре C и является её граничной точкой. Следовательно, его прообраз (кстати говоря, также лежащий на отрезке и отстоящий от образа на длину вектора сдвига) будет либо на границе B и C, либо на границе B и D. Если он на границе B и C, то возьмём также и его прообраз. Будем повторять эту операцию, пока очередной прообраз не перестанет быть на границе C и не окажется на границе D — а это произойдёт как раз на другом конце сечения. В результате мы получим цепочку прообразов, которые разбивают сечение на некоторое количество маленьких отрезочков, длина каждого из которых равняется длине вектора сдвига. Следовательно, длина сечения кратна длине вектора сдвига, ч.т.д.
Следствие из теоремы 1. Любые два сечения, являющиеся отрезками, должны быть соизмеримы.
Используя это следствие, нетрудно показать, что вертикальный параллельный перенос тоже отпадает.

Действительно, сечение раз имеет длину три клетки, а сечение два — три минус корень из двух пополам. Очевидно, эти величины несоизмеримы.
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.

| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А3 | А4 | А5 | А6 |
2. Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
3. Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата АЗ. Ответ дайте в квадратных сантиметрах.
5. Найдите отношение длины большей стороны листа к меньшей у бумаги формата А1. Ответ дайте с точностью до десятых.
1. Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А3 | А4 | А5 | А6 |
| 3 | 2 | 4 | 1 |
2. Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
Посмотрим на картинку. Если лист формата А3 разрезать пополам, то мы получим два листа формата А4. Если лист формата А4 разрезать пополам, то получим два листа формата А5. Уловили размер? Несложными логическими умозаключениями приходит к тому, что лист формата А0 состоит из 32 листов формата А5.
3. Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
Лист формата А2 состоит из двух листов формата А3, длина и ширина которых равны 420 мм и 297 мм.
Длина меньшей стороны листа формата А2 соответствует длине листа формата А3 и равна 420 мм, тогда длина большей стороны листа размера А2 равна
4. Найдите площадь листа бумаги формата АЗ. Ответ дайте в квадратных сантиметрах.
Переведем длину и ширину листа формата А3 в см.
420 мм = 42 см, 297 мм = 29,7 см
Найдем площадь: 42 · 29,7 = 1 247,4 см 2 .
5. Найдите отношение длины большей стороны листа к меньшей у бумаги формата А1. Ответ дайте с точностью до десятых.
Лист формата А1 состоит из двух листов формата А2, размеры которого мы находили в задаче №3.
Найдем размер листа А1.
Длина: 420 · 2 = 840 мм.
Ширина соответствует длине листа формата А2 и равна 594 мм.
Наконец, найдем отношение большей стороны к меньшей: для этого 840 разделим на 594.
Не можешь найти нужную задачу? Предложи свою!
Как можно разрезать прямоугольный торт на два равных куска, если кто-то уже вырезал из него прямоугольный кусок.
Есть два правильных ответа, и лучше, если вы дадите их оба. Более простой ответ находят реже, чем сложный.
Можно очень легко разрезать прямоугольник пополам — вам нужно только позаботиться о том, чтобы разрез прошел через его центр, причем под любым углом.
В данном случае у нас два прямоугольника: «позитивный» (то, что пока осталось от торта) и «негативный» (недостающий кусок). Найдите центры обоих прямоугольников и проведите через них прямую линию — это и будет линия разреза. Вы получите два равных куска.
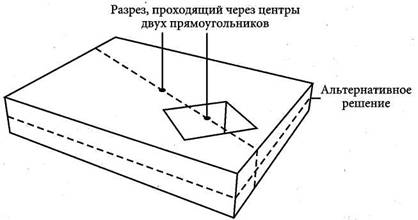
Поскольку разрез проходит через центры обоих прямоугольников, площадь двух кусков будет такова: половина площади торта минус половина площади вырезанного из торта куска. Другими словами, площадь двух кусков будет одинаковой. Это будет верным, несмотря на то, что форма кусков может быть различной.
В маловероятном случае, когда центры обоих прямоугольников оказались в одной и той же точке, можно делать разрез в любом направлении, но он, конечно, должен проходить через центр.
Альтернативное решение — резать торт не вертикально, а горизонтально, чтобы получить куски, толщина которых будет в два раза меньше, чем у целого торта, и в каждом не будет хватать одинакового по форме и площади куска. Это решение, конечно, не подходит, если торт сверху покрыт глазурью.
Какой дизайн вы предложите для туалетной комнаты Билла Гейтса?
Для ответа наэтот вопрос нужно учесть два важных обстоятельства. Во-первых, Билл Гейтс всегда может позволить себе получить то, что хочет. Во-вторых, вы должны по крайней мере предложить какие-то идеи, которые могут понравиться Гейтсу, хотя он сам об этом пока не задумывался (иначе какой смысл нанимать вас для дизайна его туалетной комнаты?).
Подразумевается, что вы усядетесь где-то вместе с Гейтсом и выслушаете, какой бы он хотел видеть свою туалетную комнату. Он сообщит вам о бюджете и сроках. Вы предложите ему много разных идей и узнаете его мнение о них. Потом вы составите план и подадите его на утверждение Гейтсу. Этот план придется не раз пересматривать, а вы, несмотря на это, должны позаботиться о том, чтобы проект уложился в срок и бюджет не был превышен. Это относится к любой задаче на разработку дизайна.
Что касается конкретных идей, которые вы предложите, имейте в виду, что вам будет трудно превзойти то, что у Гейтса уже есть в реальности. Ванная Билла Гейтса устроена так, что он может, не выходя из машины, послать команду и заполнить ее водой нужной температуры. На самом деле!
Компьютеризировать весь свой дом — это идея, к которой люди из Microsoft относятся очень серьезно. Исследовательские подразделения Microsoft разрабатывают «умные» шкафчики для лекарств и туалетных принадлежностей, которые сообщат вам, что у вас заканчивается нужное вам лекарство или туалетная бумага. «Некоторые из этих „сценариев будущего” могут показаться очень странными, признает Тед Куммер, вице-президент Microsoft по программе MSN Internet Access. — Ну, например, унитаз, который следит за здоровьем всех членов семьи, делая регулярные химические анализы, шкафчик для лекарств, который помогает заказать номер в гостинице или запереть вашу машину в гараже». «Некоторые из будущих сценариев…» Microsoft Corporation «Inside Out», стр. 271
Поэтому, если вы хотите удивить интервьюеров из Microsoft, вам вряд ли удастся это сделать, рассуждая об унитазах с электрическим подогревом. Вот несколько идей, которые им могут понравиться (это идеи футуристические, но уже сегодня их могут позволить себе богатые потребители, для которых деньги — не вопрос).
— Устройство, которое автоматически запирает шкафчики с лекарствами или средствами бытовой химии, когда в ванную входит ребенок без присмотра взрослых. В доме Гейтса уже можно отслеживать, кто находится в той или иной комнате. Идет разговор о сканировании радужной оболочки глаза и других способах быстрой и незаметной идентификации людей. Это как раз и может помочь запирать шкафчик с лекарствами от детей, «если это позволит спасти жизнь хотя бы одному ребенку», и т. д. и т. п.
— Блокнот для заметок, к которому не нужно прикасаться руками. Каждому человеку иногда приходят в голову хорошие идеи, когда он находится в туалете. Вам не захочется прикасаться к своей электронной записной книжке-«наладоннику» мокрыми руками, и если в доме Гейтса и есть такая комната, где нет компьютера, так это, наверное, туалет. Все, что вам нужно, — это устройство распознавания голоса, которое сможет записать ваше сообщение после того, как вы произнесете кодовую фразу, например «Заметки для Билла». Это устройство может автоматически отсылать записанную информацию по электронной почте к вам на работу.
– Зеркало, которое не меняет местами право и лево. Это видеоэкран и скрытая видеокамера, которые будут показывать ваше изображение таким, каким его видят другие люди, глядящие на вас. Вам будет гораздо легче пользоваться ножницами, чтобы, например, отстричь выросший не на месте волосок или подравнять усы. Если вы думаете, что эти незначительные преимущества вряд ли оправдывают отказ от «низкотехнологичного» решения, которое работает безотказно, не нуждается в новом программном обеспечении и будет работать, даже если отключится электричество… Ну, вы уверены, что действительно хотите работать в Microsoft! (У Гейтса была идея, что репродукции произведений искусства на жидкокристаллических экранах, которые вы увидите повсюду в его доме, если на них никто не смотрит, должны сливаться с деревянной отделкой стен, имитируя и фактуру дерева. Этого так и не удалось добиться. Все закончилось тем, что Гейтс заказал у столяров скользящие деревянные панели, которые могут закрывать видеоэкраны.)
Другие компании — производители программного обеспечения стали также задавать кандидатам на работу вопрос о туалетной комнате. Они, правда, часто варьируют пол и физические размеры главного героя: «Какой дизайн вы предложите для туалетной комнаты, которой будет пользоваться богатая дама, весящая сто пятьдесят килограммов?»
Дата добавления: 2018-10-26 ; просмотров: 73 ; ЗАКАЗАТЬ РАБОТУ
Ответы к странице 100 №371-380 ГДЗ к учебнику Математика 5 класс Мерзляк, Полонский, Якир
Задание № 371. Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.
Решение
Сторона наименьшего квадрата 4 см,
4 * 3 = 12 (см) – сторона наибольшего квадрата
AD = BC = 12 + 12 + 4 = 28 (см)
Стороны AD и BC состоят из 4 средних квадратов
28 : 4 = 7 (см) – сторона среднего квадрата
CD = AB = 7 + 4 * 3 = 19 (см)
Ответ: 28 см и 19 см.
Задание № 372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача.
Ответ
Задача имеет 2 решения:
1) AK = KM = MD = BN = NP = PC = 6 : 3 = 2 (см)
P ABNK = P KNPM = P MPCD = 2 * 2 + 2 * 3 = 10 (см)
2) AK = KM = MD = BN = NP = PC = 3 : 3 = 1 (см)
P ABNK = P KNPM = P MPCD = 2 * 1 + 2 * 6 = 14 (см)
Ответ: 10 см или 14 см.
Задание № 373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.
Решение
Прямоугольник ABCD со сторонами 4 см и 2 см.
Р ABCD = 2 * 2 + 2 * 4 = 4 + 8 = 12 (см)
Разделив прямоугольник пополам получим квадрат со стороной 2 см, периметр которого равен:
Р ABEF = Р FECD = 2 * 4 = 8 (см)
Ответ: 8 см – периметр каждого из квадратов.
Задание № 374. Как надо разделить квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?
Ответ
Затем из каждой пары треугольников складываем квадрат.
Задание № 375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?
Ответ
Задание № 376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?
Ответ
Задание № 377. Как надо разрезать квадрат на треугольник и четырехугольник, чтобы из них можно было сложить треугольник?
Ответ
Треугольник ставим поверх четырехугольника и получается большой треугольник.
Задание № 378. Как надо разрезать квадрат со стороной 6 см на две части по ломанной, состоящей из трех звеньев, чтобы из полученных частей можно было сложить прямоугольник?
Ответ
Задание № 379. Проведите прямую MK, луч PS и отрезок AB так, чтобы луч пересекал отрезок AB и прямую MK, а прямая MK не пересекала отрезок AB.
Задание № 380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 56 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
Поделить нацело не получится, так как в задаче опечатка. В принципе, можно решить эту задачу, используя дроби:
1) 740-(56+36+34)=614 (кг) – фруктов было бы в магазине, если бы продали 56 кг лимонов, 36 кг апельсинов и 34 кг мандаринов
2) 614_3=204 2/3 (кг) – масса каждого вида фруктов, если бы их было поровну
3) 204 2/3 +56 = 260 2/3 (кг) – лимонов имеется в магазине
4) 204 2/3 + 36 = 240 2/3 (кг) – апельсинов
5) 204 2/3 + 34 = 238 2/3 (кг) – мандаринов
Ответ: 260 2/3 кг лимонов, 240 2/3 кг апельсинов, 238 2/3 кг мандаринов
С такими данными не получается в ответе целое число. Поэтому примем количество проданных лимонов за 55 кг ( так как в прошлой редакции учебника было 55).
Решение
1) 55 + 36 + 34 = 125 (кг) – фруктов всего бы продали
2) 740 − 126 = 615 (кг) – фруктов осталось бы в магазине
3) 615 : 3 = 205 (кг) – масса каждого из оставшихся бы видов фруктов
4) 205 + 55 = 260 (кг) – лимонов имеется в магазине
5) 205 + 36 = 241 (кг) – апельсинов имеется в магазине
6) 205 + 34 = 239 (кг) – мандаринов имеется в магазине
Ответ: 260 кг лимонов, 241 кг апельсинов, 239 кг мандаринов.
Разрезания и складывания
Задача
а) Разрежьте произвольный треугольник на несколько кусочков так, чтобы из них можно было сложить прямоугольник.
б) Разрежьте произвольный прямоугольник на несколько кусочков так, чтобы из них можно было сложить квадрат.
в) Разрежьте два произвольных квадрата на несколько кусочков так, чтобы из них можно было сложить один большой квадрат.
Подсказка 1
б) Сначала составьте из произвольного прямоугольника такой прямоугольник, отношение большей стороны которого к меньшей не превышает четырех.
в) Используйте теорему Пифагора.
Подсказка 2
а) Проведите высоту или среднюю линию.
б) Наложите прямоугольник на квадрат, который должен получиться, и проведите «диагональ».
в) Приложите квадраты друг к другу, на стороне большего квадрата отмерьте отрезок, равный длине меньшего квадрата, после чего соедините ее с «противоположными» вершинами каждого из квадратов (см. рис. 1).

Решение

а) Пусть дан произвольный треугольник ABC. Проведём среднюю линию MN параллельно стороне AB, а в полученном треугольнике CMN опустим высоту CD. Кроме того, опустим на прямую MN перпендикуляры AK и BL. Тогда легко видеть, что ∆AKM = ∆CDM и ∆BLN = ∆CDN как прямоугольные треугольники, у которых равны соответствующие пара сторон и пара углов.
Отсюда вытекает метод разрезания данного треугольника и последующего перекладывания кусочков. Именно, проведём разрезы по отрезкам MN и CD. После этого переложим треугольники CDM и CDN на место треугольников AKM и BLN соответственно, как показано на рис. 2. Мы получили прямоугольник AKLB, как того и требовалось в задаче.
Отметим, что этот метод не сработает, если один из углов CAB или CBA — тупой. Так происходит из-за того, что в этом случае высота CD не лежит внутри треугольника CMN. Но это не слишком страшно: если проводить среднюю линию параллельно самой длинной стороне исходного треугольника, то в отсечённом треугольнике мы будем опускать высоту из тупого угла, а она обязательно будет лежать внутри треугольника.
б) Пусть дан прямоугольник ABCD, стороны которого AD и AB равны a и b соответственно, причём a > b. Тогда площадь того квадрата, который мы хотим получить в итоге, должна быть равной ab. Следовательно, длина стороны квадрата составляет √ab, что меньше, чем AD, но больше, чем AB.

Построим квадрат APQR, равный искомому, таким образом, чтобы точка B лежала на отрезке AP, а точка R — на отрезке AD. Пусть PD пересекает отрезки BC и QR в точках M и N соответственно. Тогда легко видеть, что треугольники PBM, PAD и NRD подобны, а кроме того, BP = (√ab – b) и RD = (a – √ab). Значит,


Следовательно, ∆PBM = ∆NRD по двум сторонам и углу между ними. Также отсюда несложно вывести равенства PQ = MC и NQ = CD, а значит, ∆PQN = ∆MCD тоже по двум сторонам и углу между ними.
Из всех приведённых рассуждений вытекает метод разрезания. Именно, сначала мы откладываем на сторонах AD и BC отрезки AR и CM, длины которых равны √ab (о том, как строить отрезки вида √ab, см. задачу «Правильные многоугольники» — врезку в разделе «Решение»). Далее, восстанавливаем перпендикуляр к отрезку AD в точке R. Теперь осталось только отрезать треугольники MCD и NRD и переложить их так, как показано на рис. 3.

Отметим, что для того, чтобы этим методом можно было воспользоваться, требуется, чтобы точка M оказалась внутри отрезка BK (иначе не весь треугольник NRD содержится внутри прямоугольника ABCD). То есть необходимо, чтобы

Если это условие не выполняется, то сначала нужно сделать данный прямоугольник более широким и менее длинным. Для этого достаточно разрезать его пополам и переложить кусочки так, как показано на рис. 4. Ясно, что после проведения такой операции отношение большей стороны к меньшей уменьшится в четыре раза. А значит, проделывая её достаточно большое число раз, в конце концов мы получим прямоугольник, к которому применимо разрезание с рис. 3.
в) Рассмотрим два данных квадрата ABCD и DPQR, приложив их друг к другу так, чтобы они пересекались по стороне CD меньшего квадрата и имели общую вершину D. Будем считать, что PD = a и AB = b, причём, как мы уже отмечали, a > b. Тогда на стороне DR большего квадрата можно рассмотреть такую точку M, что MR = AB. По теореме Пифагора  .
.

Пусть прямые, проходящие через точки B и Q параллельно прямым MQ и BM соответственно, пересекаются в точке N. Тогда четырёхугольник BMQN является параллелограммом, а так как у него все стороны равны, то это ромб. Но ∆BAM = ∆MRQ по трём сторонам, откуда следует (учитывая, что углы BAM и MRQ прямые), что  . Таким образом, BMQN — квадрат. А так как его площадь равна (a 2 + b 2 ), то это именно тот квадрат, который нам надо получить.
. Таким образом, BMQN — квадрат. А так как его площадь равна (a 2 + b 2 ), то это именно тот квадрат, который нам надо получить.
Для того чтобы перейти к разрезанию, осталось заметить, что ∆BAM = ∆MRQ = ∆BCN = ∆NPQ. После этого то, что нужно сделать, становится очевидным: необходимо отрезать треугольники BAM и MRQ и переложить их так, как изображено на рис. 5.
Послесловие
Прорешав предложенные задачи, читатель, вполне возможно, задумается над таким вопросом: а когда вообще можно один данный многоугольник разрезать прямыми линиями на конечное число таких кусочков, из которых складывается другой данный многоугольник? Немножко поразмыслив, он поймёт, что как минимум необходимо, чтобы площади этих многоугольников были равны. Таким образом, исходный вопрос превращается в следующий: правда ли, что если два многоугольника имеют одинаковую площадь, то один из них можно разрезать на кусочки, из которых складывается второй (это свойство двух многоугольников называется равносоставленностью)? Оказывается, это действительно так, и об этом нам говорит теорема Бойяи—Гервина, доказанная в 30-х годах XIX века. Более точно, её формулировка заключается вот в чём.
Теорема Бойяи—Гервина. Два многоугольника равновелики тогда и только тогда, когда они равносоставлены.
Идея доказательства этого замечательного результата заключается в следующем. Во-первых, мы будем доказывать не само утверждение теоремы, а то, что каждый из двух данных равновеликих многоугольников можно разрезать на кусочки, из которых складывается квадрат той же площади. Для этого сначала мы разобьём каждый из многоугольников на треугольники (такое разбиение называется триангуляцией). А потом каждый треугольничек превратим в квадратик (например, при помощи метода, описанного в пунктах а) и б) настоящей задачи). Осталось сложить из большого количества маленьких квадратиков один большой — это мы умеем делать благодаря пункту в).
Аналогичный вопрос для многогранников составляет одну из знаменитых проблем Давида Гильберта (третью), представленных им в докладе на II Международном конгрессе математиков в Париже в 1900 году. Характерно, что ответ на него оказался отрицательным. Уже рассмотрение двух таких простейших многогранников, как куб и правильный тетраэдр, показывает, что ни один из них не получается разрезать на конечное число частей так, чтобы из них составлялся другой. И это не случайно — подобного разрезания просто не существует.
Решение третьей проблемы Гильберта было получено одним из его учеников — Максом Деном — уже в 1901 году. Ден обнаружил инвариантную величину, которая не изменялась при разрезании многогранников на кусочки и складывании из них новых фигур. Однако эта величина оказалась различной для некоторых многогранников (в частности, куба и правильного тетраэдра). Последнее обстоятельство явно указывает на тот факт, что эти многогранники равносоставленными не являются.
Олимпиадные, логические и занимательные задачи по математике. Задачи на разрезание
В ниманию репетиторов по математике и преподавателей различных факультативов и кружков предлагается подборка занимательных и развивающих геометрических задач на разрезание. Цель использования репетитором таких задач на своих занятиях — не только заинтересовать ученика интересными и эффектными комбинациями клеток и фигур, но и сформировать у него чувство линий, углов и форм. Комплект задач ориентирован главным образом на детей 4-6 классов, хотя не исключено его использование даже со старшеклассниками. Упражнения требуют от учащихся высокой и устройчивой концентрации внимания и прекрасно подходят для развития и тренировки зрительной памяти. Рекомендуется для репетиторов математики, занимающихся подготовкой учеников к вступительным экзаменам в математические школы и классы, предъявляющие особые требования к уровню самостоятельного мышления и творческим способностям ребенка. Уровень задач соответсвует уровню вступительных олимпиад в лицей «вторая школа» (вторая математическая школа), малому Мехмату МГУ, Курчатовской школе и др.
Примечание репетитора по математике:
В некоторых решения задач, которые вы можете посмотреть щелкнув на соответствующем указателе, указан лишь один из возможных примеров разрезания. Я вполне допускаю, что у вас может получиться какая-то другая верная комбинация — не надо этого бояться. Проверьте тщательно решение вашего мылыша и если оно удовлетворяет условию, то смело принимайтесь за следующую задачу.
1) Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме части:

Подсказка репетитора по математике: Маленькие фигуры очень похожи на букву Т
Посмотреть решение репетитора по математике
2) Разрежьте теперь эту фигуру на 4 равные по форме части:

Подсказка репетитора по математике: Легко догадаться, что маленькие фигурки будут состоять из 3 клеточек, а фигур из трех клеточек не так много. Их всего два вида: уголок и прямоугольник 1×3.
Посмотреть решение репетитора по математике:
3) Разрежьте данную фигуру на 5 равных по форме частей:

Подсказка репетитора по математике:
Найдите количество клеточек, из которых состоит каждая такая фигура. Эти фигурки, похожи на букву Г.
Посмотреть решение репетитора по математике
4) А теперь нужно разрезать фигуру из десяти клеток на 4 неравных друг другу прямоугольника (или квадрата).

Указание репетитора по математике: Выделите какой-нибудь прямоугольник, а затем в оставшиеся клетки попробуйте вписать еще три. Если не получается, то смените первый прямоугольник и попробуйте еще раз.
Посмотреть решение репетитора по математкие
5) Задача усложняется: нужно фигуру разрезать на 4 разных по форме фигурки (не обязательно на прямоугольники).

Подсказка репетитора по математике: нарисуйте сначала отдельно все виды фигур разной формы (их будет больше четырех) и повторите метод перебора вариантов как в предыдущей задаче.
Посмотреть решение репетитора по математике:
6) Разрежьте эту фигуру на 5 фигур из четырех клеток разной формы таким образом, чтобы в каждой их них была закрашена только одна зеленая клетка.

Подсказка репетитора по математике: Попробуйте начать разрезание с верхнего края данной фигуры и вы сразу поймете, как действовать.
Посмотреть решение репетитора по математике:
7) По мотивам предыдущей задачи. Найдите сколько всего имеется фигур различной формы, состоящих ровно из четырех клеток? Фигуры можно крутить, поворачивать, но нельзя поднимать состола (с его поверхности), на котором она лежит. То есть две приведенные фигурки не будут считаться равными, так как они не могут получаться друг из друга при помощи поворота.

Подсказка репетитора по математике: Изучите решение предыдущей задачи и постарайтесь представить себе различные положения этих фигур при повороте. Нетрудно догадаться, что ответом в нашей задаче будет число 5 или больше. (На самом деле даже больше шести). Всего существует 7 типов описанных фигур.
Посмотреть решение репетитора по математике
8) Разрежьте квадрат из 16 клеток на 4 равные по форме части так, чтобы в каждой из четырех частей была ровно одна зеленая клетка.

Подсказка репетитора по математике: Вид маленьких фигурок не квадрат и не прямоугольник, и даже не уголок из четырех клеток. Так на какие же фигуры надо попытаться разрезать?
Посмотреть решение репетитора по математике
9) Изображенную фигуру разрежьте на две части таким образом, чтобы из полученных частей можно было сложить квадрат.

Подсказка репетитора по математкие: Всего в фигуре 16 клеток — значит, квадрат будет размеро 4×4. И еще как-то нужно заполнить окошко в середине. Как это сделать? Может быть каким-нибудь сдвигом? Тогда поскольку длина прямоугольника равна нечетном учислу клеток, разрезание нужно провести не вертикальным разрезом, а по ломаной линии. Так, чтобы верхняя часть отрезалась с одной стороны от средние клетки, а нижняя с другой.
Посмотреть решение репетитора по математкие
10) Разрежьте прямоугольник размером 4×9 на две части с таким расчетом, чтобы в результате из них можно было сложить квадрат.

Подсказка репетитора по математике: Всего в прямоугольнике 36 клеток. Поэтому квадрат получится размером 6×6. Так ка кдлинная сторона состоит из девяти клеток, то три из них нужно отрезать. Как дальше пойдет этот разрез?
Посмотреть решение репетитора по математике
11) Крестик из пяти клеток, показанный на рисунке требуется разрезать (можно резать сами клетки) на такие части, из которых можно было бы сложить квадрат.
Подсказка репетитора по математике: Понятно, что как бы мы по линиям клеточек не резали — квадрат не получим, так как клеток всего 5. Это задача единственная, в которой разрешается резать не по клеткам. Однако их все равно хорошо бы оставить в виде ориентира. например, стоит заметить, что нам как-то нужно убрать углубления, которые у нас есть — а именно, во внутренних углах нашего креста. Как бы это сделать? Например, срезая какие-то выпирающие треугольники из внешних уголков креста.
Посмотреть решение репетитора по математике:
Комментарий к решению: разрежьте так ка кпоказано на рисунке и вставьте голубые треугольники в пустые области, показанные фиолетовыми треугольниками.
Колпаков Александр Николаевич. Репетитор по математике Москва, Строгино.
Классный сайт! Спасибо за самые интересные во всём интернете задачи с ответами!










